A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
At time 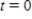 minutes, the temperature of an object is
minutes, the temperature of an object is 
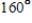 F. The temperature of the object is changing at the rate given by the differential equation
F. The temperature of the object is changing at the rate given by the differential equation 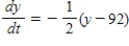 . Use Euler's Method to approximate the particular solutions of this differential equation at
. Use Euler's Method to approximate the particular solutions of this differential equation at 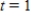 . Use a step size of
. Use a step size of 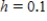 . Round your answer to one decimal place.
. Round your answer to one decimal place.
A) 137.1
B) 139.5
C) 147.4
D) 144.6
E) 132.7
G) C) and D)
Correct Answer

verified
E
Correct Answer
verified
Multiple Choice
The logistic function 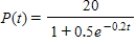 models the growth of a population. Identify the value of k.
models the growth of a population. Identify the value of k.
A) 1.7
B) 2.2
C) 0.2
D) 20
E) 0.5
G) C) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the differential equation. 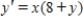
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the general solution of the differential equation 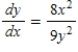 .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether the function  is homogeneous and determine its degree if it is.
is homogeneous and determine its degree if it is.
A) homogeneous, the degree is 3
B) homogeneous, the degree is 4
C) not homogeneous
D) homogeneous, the degree is 2
E) homogeneous, the degree is 1
G) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A conservation organization releases 20 wolves into a preserve. After 2 years, there are 35 wolves in the preserve. The preserve has a carrying capacity of 125. Determine the time it takes for the population to reach 80.
A) 9.020 years
B) 4.875 years
C) 6.259 years
D) 3.692 years
E) 7.884 years
G) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A 300-gallon tank is full of a solution containing 55 pounds of concentrate. Starting at time  distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as
distilled water is added to the tank at a rate of 30 gallons per minute, and the well-stirred solution is withdrawn at the same rate. Find the quantity of the concentrate in the solution as  .
.
A) 30
B) 56
C) 55
D) 0
E) 1
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Match the logistic differential equation and initial condition with the graph of its solution shown below. 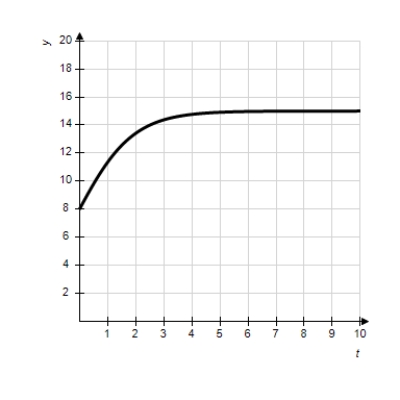
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The initial investment in a savings account in which interest is compounded continuously is $803. If the time required to double the amount is 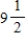 years, what is the annual rate? Round your answer to two decimal places.
years, what is the annual rate? Round your answer to two decimal places.
A) 7.30 %
B) 7.70 %
C) 13.71 %
D) 6.10 %
E) 8.70 %
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the function 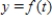 passing through the point
passing through the point 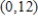 with the first derivative
with the first derivative 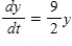 .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) B) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The number of bacteria in a culture is increasing according to the law of exponential growth. After 2 hours there are 135 bacteria in the culture and after 4 hours there are 390 bacteria in the culture. Answer the following questions, rounding numerical answers to four decimal places. (i) Find the initial population. (ii) Write an exponential growth model for the bacteria population. Let t represent time in hours. (iii) Use the model to determine the number of bacteria after 8 hours. (iv) After how many hours will the bacteria count be 25,000?
A) (i) 46.7341; (ii) ![]() ; (iii) 4,566.8441; (iv) 14.1787 hr
; (iii) 4,566.8441; (iv) 14.1787 hr
B) (i) 48.8841; (ii) ![]() ; (iii) 5,941.5613; (iv) 16.4067 hr
; (iii) 5,941.5613; (iv) 16.4067 hr
C) (i) 46.7341; (ii) ![]() ; (iii) 3,254.11; (iv) 11.8442 hr
; (iii) 3,254.11; (iv) 11.8442 hr
D) (i) 52.5141; (ii) ![]() ; (iii) 8,693.0147; (iv) 18.5179hr
; (iii) 8,693.0147; (iv) 18.5179hr
E) (i) 54.0741; (ii) ![]() ; (iii) 11,345.4782; (iv) 20.2973 hr
; (iii) 11,345.4782; (iv) 20.2973 hr
G) A) and B)
Correct Answer

verified
C
Correct Answer
verified
Multiple Choice
The logistic function 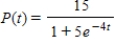 models the growth of a population. Determine when the population reaches one-half of the maximum carrying capacity. Round your answer to three decimal places.
models the growth of a population. Determine when the population reaches one-half of the maximum carrying capacity. Round your answer to three decimal places.
A) 0.402
B) 3.000
C) 0.677
D) 7.500
E) 2.000
G) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Sketch a few solutions of the differential equation on the slope field and then find the general solution analytically. 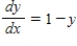
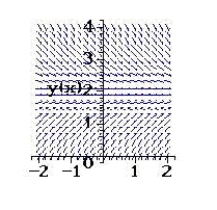
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use Euler's Method to make a table of values for the approximate solution of the following differential equation with specified initial value. Use 5 steps of size 0.05. 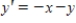 ,
, 
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) D) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Write and solve the differential equation that models the following verbal statement. Evaluate the solution at the specified value of the independent variable, rounding your answer to four decimal places:
The rate of change of Q is proportional to Q. When  ,
, 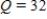 and when
and when 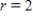 ,
, 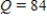 . What is the value of Q when
. What is the value of Q when  ?
?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) B) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Each of the following graphs is from a logistic function 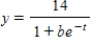 . Which one has the smallest value of b?
. Which one has the smallest value of b?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) B) and D)
Correct Answer

verified
E
Correct Answer
verified
Multiple Choice
A 300-gallon tank is half full of distilled water. At time  , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 6 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 4 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 6 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 4 gallons per minute. At the time the tank is full, how many pounds of concentrate will it contain? Round your answer to two decimal places.
A) ![]() lbs
lbs
B) ![]() lbs
lbs
C) ![]() lbs
lbs
D) ![]() lbs
lbs
E) ![]() lbs
lbs
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use integration to find a general solution of the differential equation 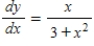 .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
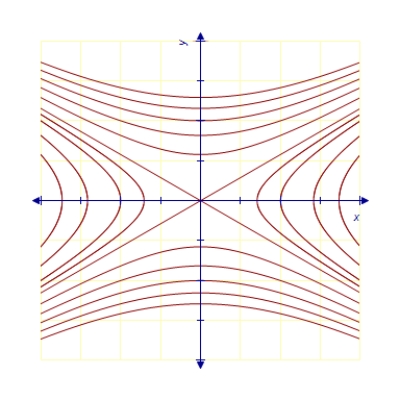
Find the orthogonal trajectories of the family 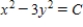 .
. 
A) ![]()
![]()
B) ![]()
![]()
C) ![]()
![]()
D) ![]()
![]()
E) ![]()
![]()
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Showing 1 - 20 of 93
Related Exams